Math Camp Summer 2026

Check back for more information about Math Summer Camp 2026!

Face-to-Face Math Camps

A week of math adventures awaits 4th through 7th grade students! Math is more than just numbers and this fun and exciting program is designed to spark interest in any student. Campers will engage in fascinating games and hands-on activities that will reinforce mathematical concepts, thinking skills, and problem-solving abilities. We will explore game theory, rocket flight, video games, code breaking, and more, with all the explorations designed to uncover the relevance of mathematics in daily life.

Tentative Schedule:

June 8 - 12, 2026

9am - 12pm: Rocket Camp

1pm - 4pm: Bridge Camp

June 16 - 19, 2026

9am - 12:30pm: Bridge Camp

1pm - 4:30pm: Rocket Camp

June 22 - 26, 2026

9am - 12pm: Rocket Camp

1pm - 4pm: Bridge Camp

Location:

McKay Education Building

$Map to McKay Education Building$

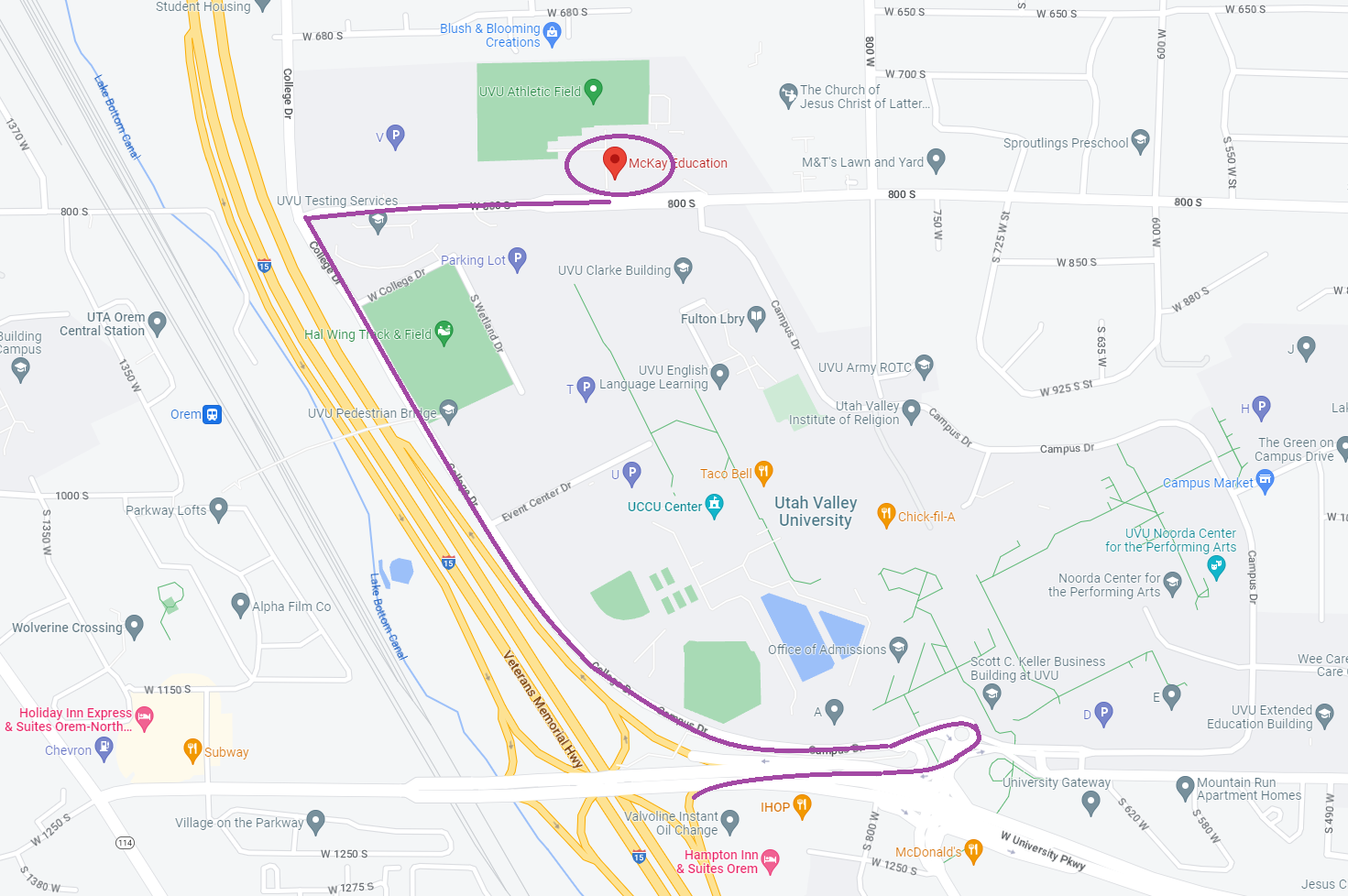
This is a map to get to the McKay Education building from I-15. Exit the highway and head toward the university (East side of the highway) and take the two lanes on the left to enter campus. You will go around the round-about and exit at the third exit onto Campus Drive. Take Campus Drive to 800 South (Second light). Turn right onto 800 South and follow it to the McKay Education Building (north side of the road) and turn left into the parking lot.

What are Parents Saying?

I heard the word "love" and "math" in the same sentence. Thank you!

My daughter actually seemed very excited about math with a whole new outlook!

My son came home excited every day to learn about math in a fun way.

There are numerous youth sport camps in Utah Valley during summer time. It's about time to have something academic held for kids who are inclined towards academic.

My kids loved it. Math was fun the way you taught it and used the games. They enjoyed it a lot.

Contact

If you have any questions or concerns please contact Dr. Lindsey Gerber

Loading Directory data....

Math Camp Activities

Are you golden

Participants will measure the length of different body parts and compare the ratios of lengths to discover if the Golden Ratio is present in their own bodies.

Code Breaking Basics

Students are introduced to a basic cipher then use that cipher to decode clues that lead to a treasure.

Radioactive M&Ms

Using M&Ms students model radioactive decay and growth and gain a general understanding of half-life and doubling.

Game Theory

Students will gain a general idea the field of mathematics called Game theory. They will begin by playing two famous games, The Prisoners’ Dilemma and Nuclear War. They will address equilibrium points and learn about outcomes.

Fractals!

What is a fractal? How is it created? Students answer these questions by exploring the Sierpinski triangle and its construction. We construct the Sierpinski triangle both classically and by using L-Systems, leading to a natural investigation of fractal dimension.

Wii™ Bowling

Explore order of operations and the measures of central tendency (mean, median and mode) by bowling 10 frames.

Bubble Mania

We investigate the conservation of energy by using shape skeletons and looking at the bubble film that is created in them.

Solar System Running

How far away is Pluto? We will explore distance, rate and time, as well as thinking about very large numbers, by “running” to Pluto.

Math Magic

Students will create their own math magic trick after learning how they work and what makes a magic trick successful.

Mastodon Game

Grow your own Mastodon Herd by using set outcomes of a regular die. We will explore how probability affects outcomes in a random number game.

The Basics of Fractals

We explore self-similarity using different mediums. Students make their own fractals and see how fractals are present in our world.

Lemonade Game

How do you make the most money in your summer lemonade stand? Look at optimization by operating a lemonade stand.

Pythagorean Theorem with Jelly Beans

Students are asked to explore and examine a variety of geometric shapes and discover their characteristics and properties using jelly beans. They also create inductive arguments about the Pythagorean Theorem.

Mental Math

We look at tricks to multiply numbers very quickly in your head, then the students race each other to see who is the fastest mental multiplier.

Card Tricks

Using probability and binary numbers, we lead students through a number of card tricks that can be completed using math.

Fractions and Cooking

We will make ice cream while exploring what fractions really mean. This will include fraction division and multiplication and reasonable answers for why we do arithmetic the way that we do.

Graph Theory

Explore the basics of Graph Theory including several games that involve tracing figures without redrawing the lines. Why do some shapes work and others do not? Our activity will involve a discussion on nodes and some of Euler’s work.

Modular Arithmetic

Learn how to count modularly and beat everyone else at a game of speed where the winner must count forwards and backward the fastest.

Survey of the Solar System

Gain an understanding of the size of the Solar System by scaling it down. We explore scaling by using a ratio to scale down the solar system to fit in a soccer field. Students will gain an understanding of very large numbers and how to scale.

Math Games

We play several math games to increase enthusiasm for basic arithmetic and to develop skills.